Illustrating Multi-objective Optimisation Evolutionary Algorithm

I. Introduction

Problems with multiple objectives that conflict with each other widely exist in real life and are often referred to as multi-objective optimisation problems (MOPs) [1]. An MOP is formulated as

$minimize \ f(x) = \{f_1(x),\dots, f_m(x)\}$

where $x$ is a solution in the decision space, $f(x)$ is an $m$-objective function and $f_i(x)$ refers to the $i^{th}$ objective with $i \in \{1,\dots,m\}$. $x$ is said to $x'$ if $x$ is no worse than $x'$ in all the $m$ objectives and there exists at least one objective $i$ on which $f_i(x) < f_i(x')$. Among a set of solutions $P$, the non-dominated solution set is a set of solutions that are not dominated by any member of $P$. Therefore, different from single-objective optimisation problems, the optima is a set of solutions, called Pareto-optimal set, instead of one single solution. Pareto-optimal set is a non-dominated set of the entire decision space. Each solution of Pareto-optimal set reveals a trade-off between $m$ objectives. The quality of approximated Pareto set often falls into four aspects, namely convergence, spread, uniformity and cardinality [2].

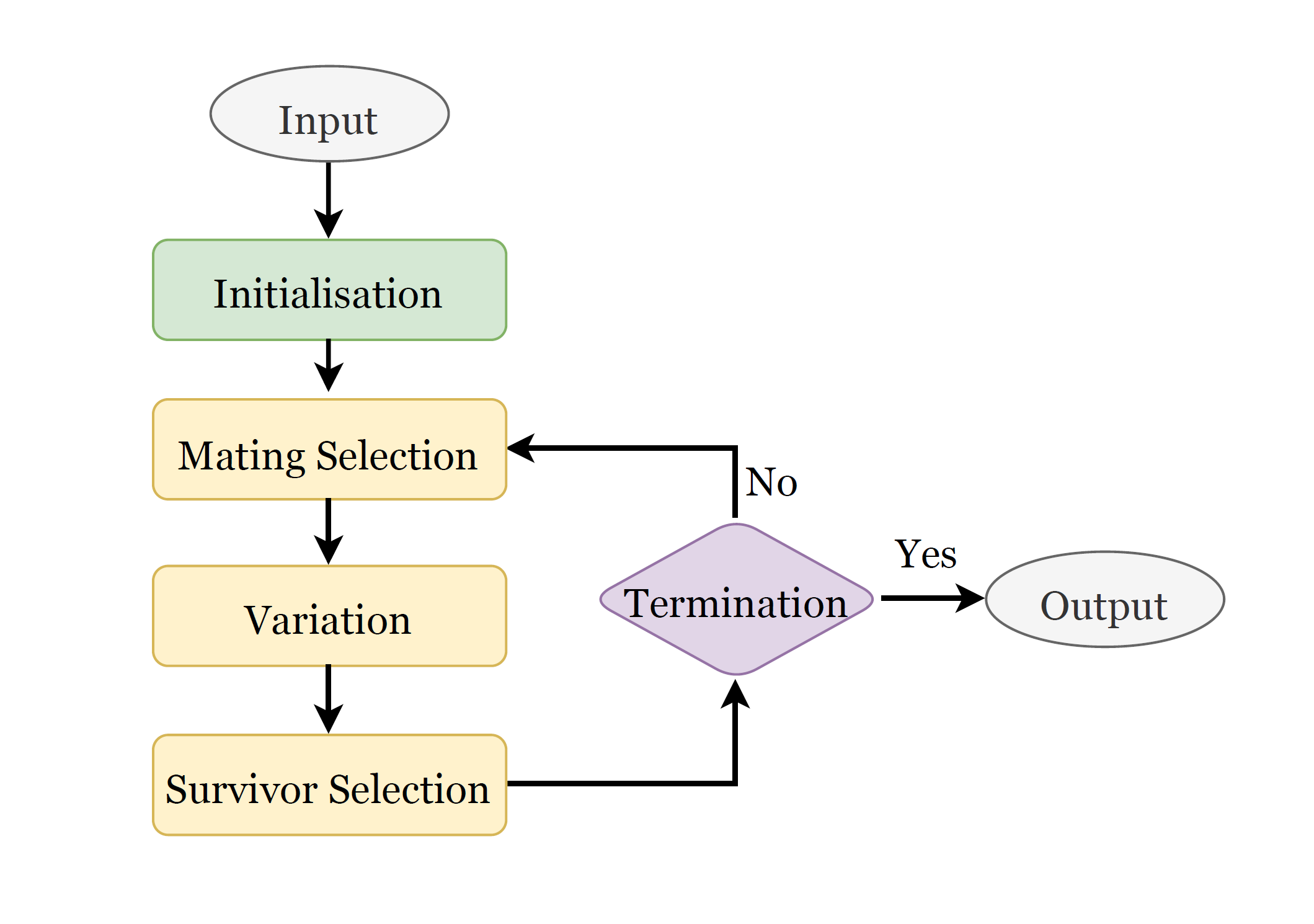
Multi-objective evolutionary algorithms (MOEAs) are population-based, black-box optimisation methods, which are very suitable for solving complex MOPs. The common underlying idea of MOEAs is to evolve a solution set, also called population, from generation to generation to converge to the Pareto set, following the rule of survivor-of-the-fittest. Each solution in a population is called an individual. Quality of each solution can be denoted as fitness in the context of MOEAs. The optimisation process of MOEAs generally includes three components, mating selection, variation and survivor selection. Those three components can guide the evolution of a maintained solution set to better approximate the Pareto-optimal set.

Non-dominated Sorting Genetic Algorithm II (NSGA-II) [3] is a well-known MOEA, which uses the fast non-dominated sorting method and crowding distance estimation to assess solutions. The algorithm works by generating a population of candidate solutions, also known as individuals, which represent potential solutions to the problem. Each individual has a set of variables that can be adjusted to optimize the objectives of the problem.

The algorithm then evaluates each individual's fitness based on how well it satisfies the objectives of the problem. The fitness function is usually defined as a combination of the multiple objectives, taking into account their relative importance or trade-offs.

The algorithm then selects the best individuals based on their fitness and uses them to create a new population of candidate solutions. This process is repeated over multiple generations, allowing the algorithm to converge towards the optimal solution to the problem.

One of the key advantages of multi-objective optimisation evolutionary algorithms is their ability to handle multiple conflicting objectives simultaneously. By using a fitness function that considers all the objectives, the algorithm can find a set of solutions that represent the optimal trade-offs between the different objectives.

These algorithms can also handle both continuous and combinatorial optimisation problems, making them versatile for a wide range of applications.

Figure 1: General framework of MOEAs.

II. Two Types of MOPs: ZDT1 and MOTSP

In this work, two types of classic MOPs are considered to illustrate the optimisation process of MOEAs, a numerical problem, ZDT1 [4], and a combinatorial problem, travelling salesman problem (MOTSP) [5]. ZDT1 is a bi-objective problem from the ZDT test suite [4]. A solution to ZDT1 is a four-dimensional vector in the continuous space. MOTSP [5] is a bi-objective combinatorial problem. Given a set of cities, MOTSP aims to find a route which visits every city exactly once and returns to the depart city. Two kinds of costs, fuel consumption and time cost, are caused when travelling between any pair of cities. Travelling between two cities may cost less fuel but longer travel time due to the traffic congestion. A solution to MOTSP is a route, represented by a combinatorial permutation sequence.

III. A CLASSIC MOEA: NSGA-II

This section describes the three components of MOEAs, namely mating selection, variation, and survivor selection. All these components are operations of a set of population.

Population size: Population size is a parameter used in evolutionary algorithms to define the number of candidate solutions, or individuals, that are generated and evaluated at each generation of the algorithm.

Mating Selection

The aim of mating selection is to differentiate and select some promising individuals as parents based on their fitness. The process of mating selection involves a probabilistic approach, with which the individuals with higher fitness are more likely to be selected as parents. Fitness assignment in NSGA-II involves two key steps, nondominated sorting and crowding distance estimation [3]. In the nondominated sorting step, solutions are ranked at different nondomination front levels. For two solutions on the same non-domination front, the estimation of crowding distance is considered as fitness to further distinguish different solutions on the same front.

Variation

The purpose of variation, also called reproduction, is to generate new solutions based on the promising parents chosen according to the mating selection. Newly generated solutions are excepted to inherit good information from their parent solutions. Crossover and mutation are two common types of search operators in evolutionary algorithms.

Figure 4: Crossover operation in Numerical Optimisation and in Permutation Optimisation

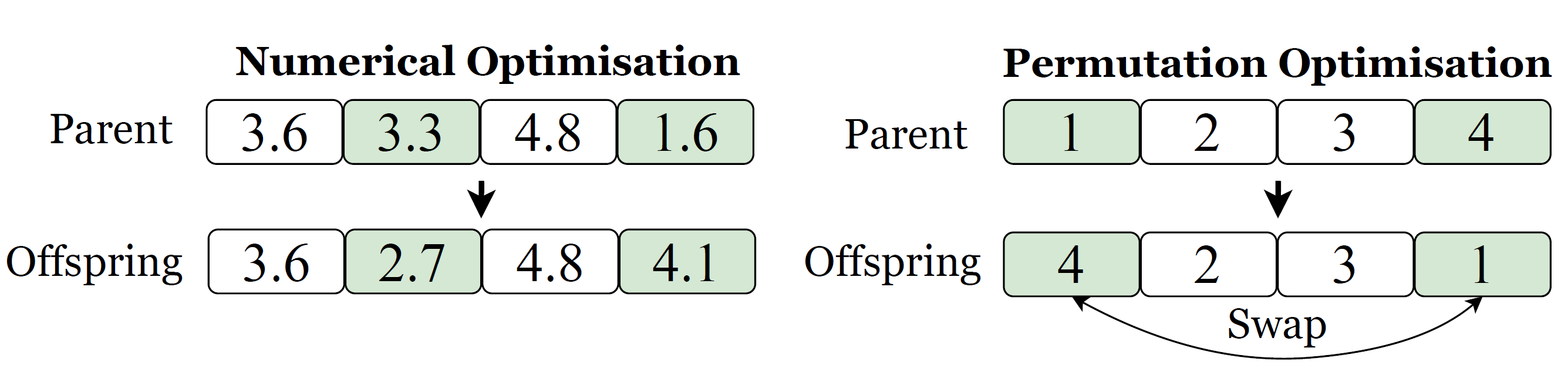
Crossover aims to keep and recombine good building blocks of the parents. By exchanging numbers in Parent 1 and Parent 2, two offspring are generated. Fig. 1 illustrates examples of crossover on real-valued and permutation-based solution representations, respectively. Especially, additional operations, such as mapping operation, may be necessary to make a permutation-based solution feasible, as shown in the right figure of Fig. 1.

Figure 5: Mutation operation in Numerical Optimisation and in Permutation Optimisation

Mutation aims to explore new area in decision space and possibly escape from local optima. Adding a small noise is a widely used mutation strategy. Different mutation strategies have been designed to improve the exploration ability. In Fig. 2, two different strategies are applied to these real-valued and permutation-based solutions. Green blocks are mutated to form new groups as offspring groups and the other blocks remain the same to maintain the quality. On the left of Fig. 2 (real-valued solutions), some of the numbers change in a certain range. When mutating permutation-based solutions (right of Fig. 2), a mutation operator called swap is illustrated.

Survivor Selection

Survivor selection, also known as the environmental selection, determines which individuals among the current population and offspring will survive and form the population in the next generation. Hence, the population is expected to converge towards the Pareto-optimal set. The fitness assignment of NSGA-II in survivor selection is the same as that of mating selection.

IV. Manual

In evolutionary algorithms, a survivor selection step is crucial to determine which individuals from the current population will be carried over to the next generation. Traditionally, survivor selection is based on certain criteria, such as fitness or objective values, which are automatically calculated by the algorithm. However, by designing a user-defined feature, we can empower users to manually select individuals from the population that they wish to retain during the survivor selection phase.

This user-defined feature allows users to have more control over the evolutionary process in this immersive article by manually selecting individuals based on their specific requirements and domain knowledge. For example, users can choose to retain individuals that appears bad to check its evolutionary process. This manual selection can guide the algorithm towards evolving solutions that are more aligned with the user's expectations and desired solution space.

By incorporating this user-defined feature, the evolutionary algorithm becomes more customizable and adaptable to the user's preferences and problem domain, allowing for a more personalized and guided optimization process. Overall, this feature empowers users to actively participate in the evolutionary process.

V. CONCLUSION

This paper describes three main components of MOEAs, i.e., mating selection, variation and survivor selection. A numerical and a combinatorial problems and NSGA-II are selected as case studies to illustrate how MOEAs work